Inertial sensors are used to transduce inertial force into measurable electrical signals to measure an object’s acceleration, inclination, and vibration. Micromachining technology has made it possible to produce MEMS (Micro Electromechanical System) inertial sensors using single-crystal silicon sensor elements. These micron-sized sensors meet all major system design drivers like low cost, high performance, high precision, and small form factor. Based on the same principles as macroscopic inertial sensors, MEMS inertial sensors can detect the slightest change in position, orientation, and acceleration of an object several meters long using a sensor unit as small as a few micrometers in dimensions.

There are mainly two types of MEMS inertial sensors — accelerometers that measure linear acceleration in one or more axis, and gyroscopes that measure angular motion. These sensors are manufactured for specific applications, requiring inertial sensors with different bandwidths, resolutions, and dynamic ranges. For example, the inertial sensor used in the automotive airbag release system must have a capacity of up to 0.5 KHz, a resolution of around 500 mG, and a dynamic range of about +/-100G. While inertial sensor used in a space microgravity measurement instrument can have a bandwidth of 0-10 Hz, but must have a resolution as precise as < 1 µG  and dynamic range less than +/- 1G.

Inertial sensors are generally part of a larger control system in any application or device. Mere information on an object’s acceleration or angular movement is useless. The information collected from an inertial sensor is always used to control the movement of the device itself or to activate an actuator, like opening a car’s airbag.

Applications of inertial sensors
Building inertial sensors was once costly and restricted to military and aerospace applications. The development of MEMS inertial sensors has opened the possibilities for using them in automotive and various consumer electronics segments.

In the automotive industry, an accelerometer is used for airbag release control, traction control, seat belt control, active suspension, the antilock braking system (ABS), and monitoring vehicle vibrations. The gyroscope is used for rollover protection, automatic indicators, power steering, and vehicle dynamics.

In the consumer segment, inertial sensors are used in a variety of applications, such as platform stabilization in video cameras, virtual reality headsets, pointing devices for computers, intelligent toys, and gaming keypads. Nowadays, all smartphones and tablets have inertial sensors for detecting screen rotation, gaming, and augmented reality applications.

Inertial sensors also monitor the position and orientation of robotic manipulators and unmanned robotic vehicles. In medical applications, these sensors monitor patients with specific conditions, such as patients with Parkinson’s disease. High-end inertial sensors are used in military and aerospace applications like smart ammunition, aircraft dynamics control, crash detection, seat ejection systems in aircraft, and microgravity measurement.

Accelerometers
Accelerometers consist of a mechanical sensing element that can measure acceleration in one or more axes. The sensing element consists of a proof mass attached to a reference frame by a mechanical suspension system. In MEMS sensors, the proof mass is an extremely small seismic mass, and the suspension system is built from silicon springs.

The proof mass deflects from its stable position whenever the sensor experiences some inertial force due to acceleration. Newton’s second law of motion governs this. The deflection of the proof mass to acceleration is expressed by a Laplace equation as follows:
x/a = 1/(s² + b/m + s*k/m)
Where,
x is the displacement of the proof mass,
a is acceleration,
s is Laplace operator,
b is the damping coefficient,
m is the mass of the proof mass,
k is the mechanical spring constant of the suspension system.

The following equation gives the resonant frequency of the sensor:
f_n = √(k/m)

The following equation gives the quality factor:
Q = √(m*k)/b

The following equation gives the sensitivity of the sensor (in the open loop):
S = m/k

You can see, then, that if the sensitivity is increased, resonant frequency decreases, and vice versa. This trade-off can be adjusted with a closed-loop system. The damping coefficient determines the maximum bandwidth of the accelerometer. In MEMS accelerometers, the damping coefficient is often variable and increases with a proof mass displacement.

In all types of micro-machined accelerometers, the displacement of the proof mass is measured by position-measuring interfaces. For example, in a capacitive measurement, movable plates are attached to the proof mass and move along it between fixed capacitive electrodes. Many types of sensing mechanisms are used in the design of accelerometers. Some of the common sensing methods include piezoresistive, capacitive, piezoelectric, optical, and tunneling current.

The accelerometer can have an open-loop or closed-loop system. If the electrical signals from the position measurement interface are directly used as the output signals, it is called an open-loop accelerometer. Most accelerometer sensors are open-loop because they are easy to build. However, open-loop accelerometers have to be managed with high tolerances due to variable spring constant, variable damping coefficient, and non-linear proof mass displacements.

In a closed-loop accelerometer, a feedback system applies a feedback force to the proof mass proportional to its acceleration, returning the proof mass to its resting position. This way, the non-linear factors are canceled out, sensitivity becomes dependent on the feedback control, and the dynamics of the sensor can be precisely controlled using an electrical signal controller. The proof mass can return to its resting position using electrostatic, thermal, or magnetic actuation. The feedback signal controlling the feedback force can be analog or digital. All this adds more complexity to the sensor design.

Acceleration sensing methods
There are many ways in which accelerometers sense acceleration in a particular axis. Some of the acceleration sensing methods are described below:

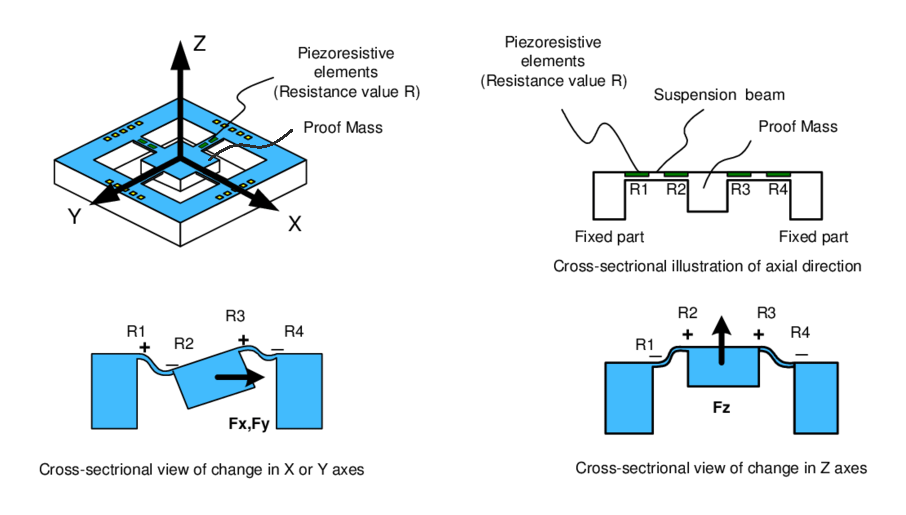
1. Piezoresistive Accelerometers – In these types of accelerometers, the proof mass is attached to a piezoresistor. The resistor is connected to a read-out electronic circuit. When there is displacement in proof mass, there is a change in the resistance of the piezoresistor proportional to the applied force. These types of accelerometers are the first ones to see bulk production. The biggest drawback of these types of accelerometers is their thermal stability. The piezoresistance can significantly change due to thermal noise and can lead to false outputs.

   

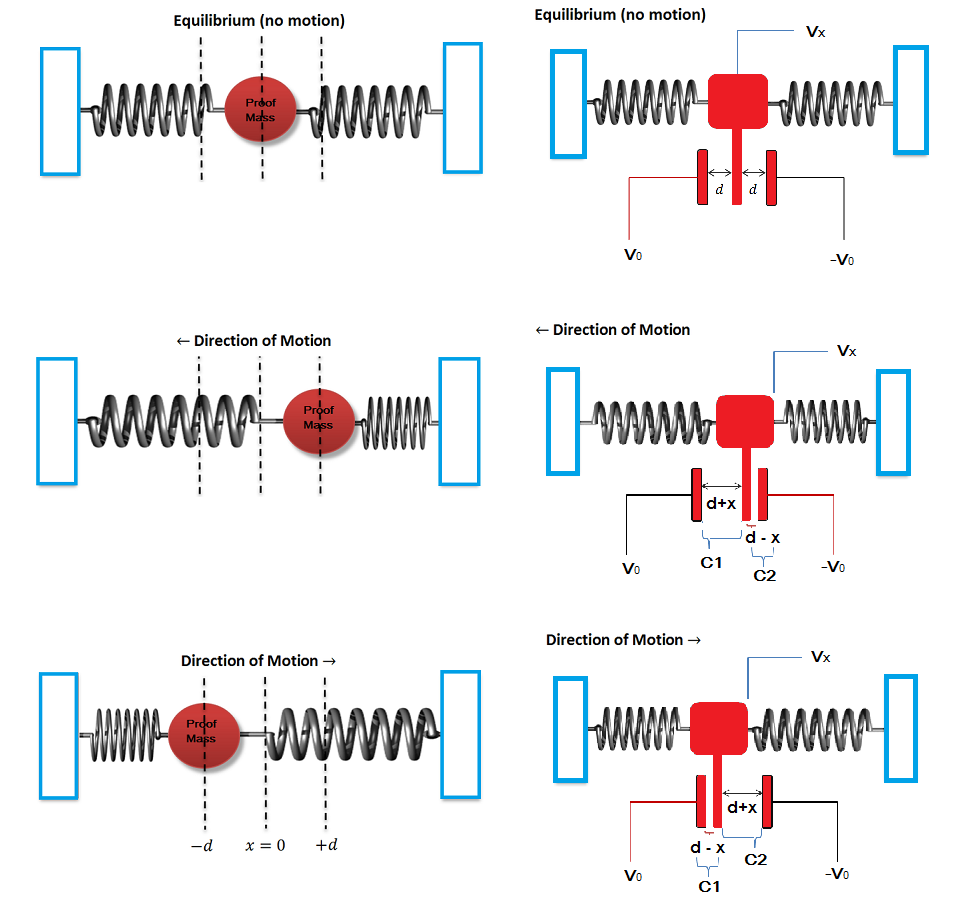
2. Capacitive Accelerometers – In capacitive accelerometers, capacitive sense fingers are attached to the proof mass, which moves along a given axis with the displacement of the proof mass. Each movable plate is placed between two electrodes. When there is an acceleration, the proof mass is displaced in the opposite direction of motion, and the variable plate moves along the proof mass. The change in the position of a variable plate along an axis causes a change in its distance with fixed electrode plates and causes a symmetrical change in capacitance. This is then measured as electrical output by a read-out electronics. The capacitive accelerometers are thermally stable but are prone to electromagnetic interference, where they can give false outputs due to parasitic capacitance.

   

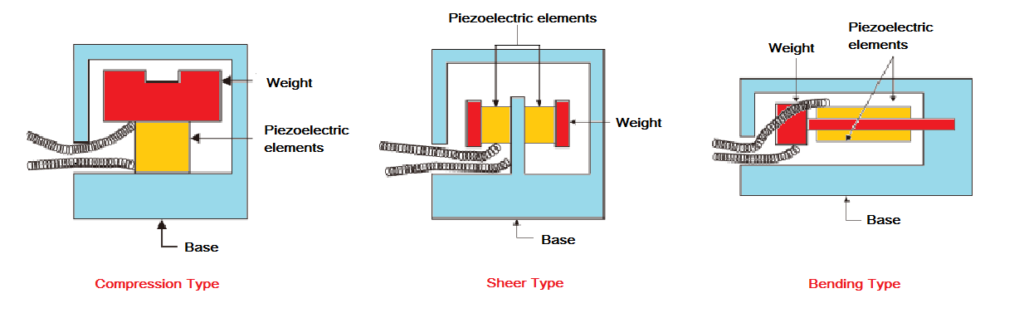
3. Piezoelectric Accelerometers—Most macroscopic accelerometers use piezoelectric materials to detect the motion of proof mass. Many micro-machined accelerometers also use the same principle. These accelerometers have great bandwidth but extremely poor resonant frequency due to leakage currents. The piezoelectric material produces electrical signals proportional to the displacement of the proof mass in a given axis.

   

4. Tunnelling Accelerometers – These types of accelerometers use tunneling current to measure the displacement of the proof mass. The tunneling current between a sharp tip and an electrode changes exponentially by the tip-electrode distance. The following equation gives the tunneling current:

I = I₀ * exp(-ᵦ√(φz))

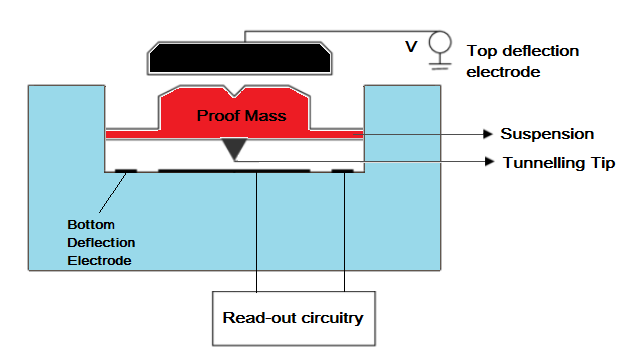
Where,
I is Tunnelling current between tip and electrode,
I₀ is scaling current depending upon the material used,
ᵦ is a conversion factor,
φ is tunnel barrier height in eV,
and z is tip-electrode distance.

5. Resonant Accelerometers—In a resonant accelerometer, the proof mass is attached to a resonator. The displacement of the proof mass changes the strain of the resonator and, thus, its resonant frequency. The change in frequency is converted to digital electrical signals using a frequency counter circuit. These accelerometers are quite immune to noise and are highly reliable, as frequency changes can be directly converted to digital format.

   

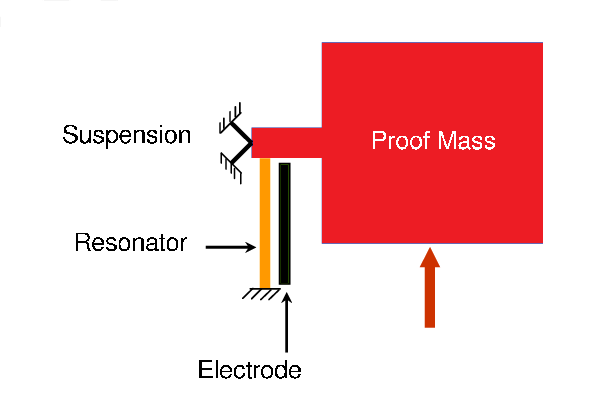
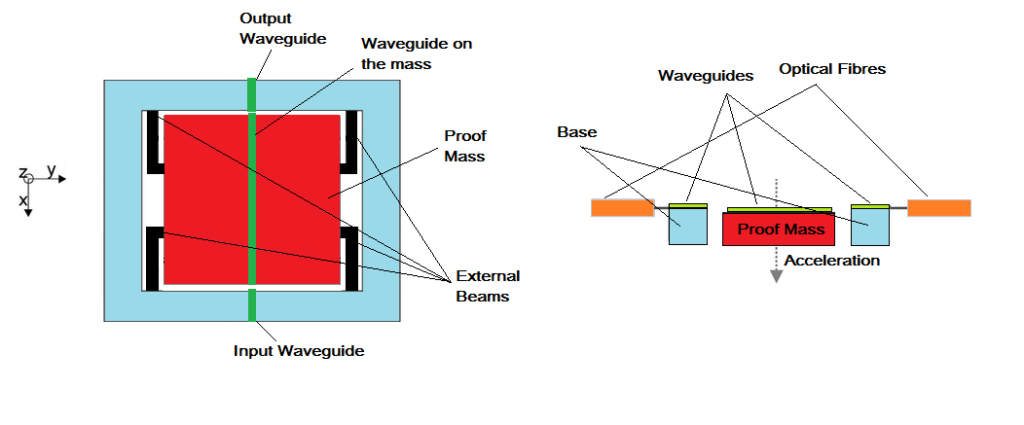
6. Optical Accelerometers – These accelerometers use optical fibers and waveguides attached to the proof mass. However, optical fiber-type accelerometers are unsuitable for batch fabrication as the fiber must be manually installed near the proof mass in the sensor assembly. Another type of optical accelerometer uses LED and PIN photodetectors to measure the displacement of the proof mass. The optical accelerometers have the advantage that they are free from electrostatic and electromagnetic interference. But, because they usually involve a complex assembly and read-out circuitry, they are not very popular.

   

Gyroscopes
A gyroscope measures the rotation of an object. The MEMS gyroscopes use the principle of Coriolis force. When a mass moves in a rotating system, it experiences a force perpendicular to the axis of rotation and the direction of motion. This is called the Coriolis force. A MEMS gyroscope consists of a mechanical structure that is driven into resonance due to Coriolis force and excites secondary oscillation in the same or a secondary structure. The secondary oscillation is proportional to the rotation of the structure in a given axis.  The Coriolis force has a relatively small amplitude compared to its driving force. That is why all MEMS gyros use a vibrating structure that uses the phenomenon of Coriolis force.

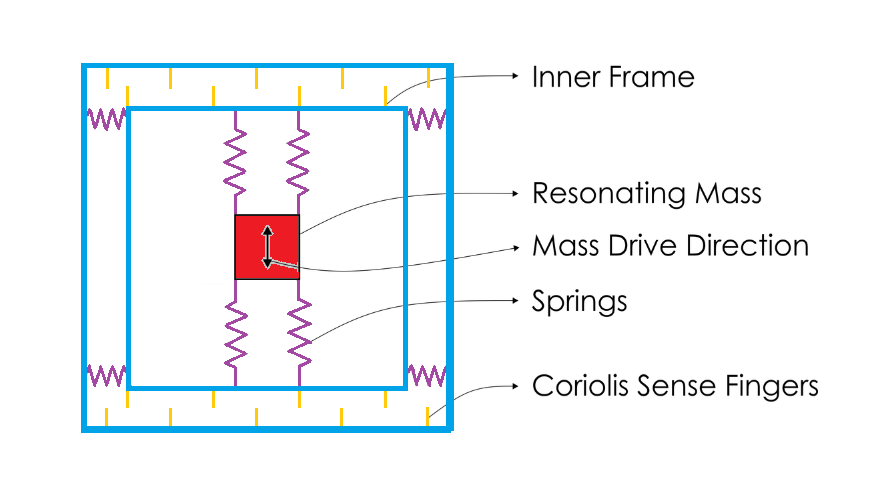
The vibrating structure consists of a proof mass connected to an inner frame by a pair of springs. Another set of orthogonal springs connects The inner frame to an outer frame. There are capacitive sense fingers between the inner frame and the outer frame attached along the orthogonal springs. The Coriolis force is proportional to both the angular velocity of the rotating object and the object’s velocity towards or away from the axis of the rotation. The proof mass is continuously driven sinusoidally along the inner springs. When the system experiences rotation, the resonating proof mass experiences Coriolis force along the orthogonal springs attached between the inner and outer frame. This changes the distance between the capacitive sense fingers, so an electrical signal proportional to Coriolis force is output. As the Coriolis force is proportional to angular velocity, the electrical signal due to it is also proportional to the angular velocity of the system.